We can visualize addition using sets:
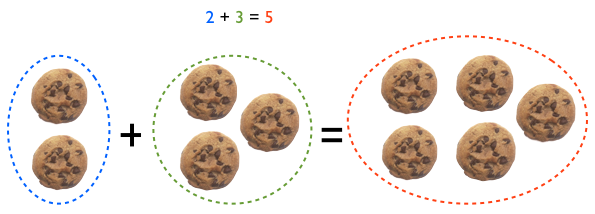
We had 2 cookies and received 3 more so now we have 5 cookies
or the number line:
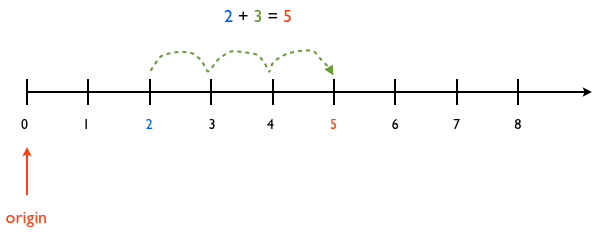
Starting at location 2 we advance 3 steps to end in location 5
Adding values with units
We can only simplify the addition of unit-less items, or of items that have the same units. For example, we can simplify the addition of unit-less items:
$$
5 + 3 = 8
$$
and the addition of items with the same units
$$
5\mbox{ cookies } + 3\mbox{ cookies } = 8\mbox{ cookies }
$$
but we cannot simplify the addition of unit-less items to items with units:
$$
5 + 3\mbox{ cookies } = 5 + 3\mbox{ cookies }
$$
or the addition of items with different units:
$$
5\mbox{ cookies } + 3\mbox{ marbles } = 5\mbox{ cookies } + 3\mbox{ marbles }
$$
Describing an addition
Although the following two forms describe the same addition process, sometimes it is easier to solve a problem using one form than the other.
$$
a + b = x
$$
is the same as
$$
\begin{align}
a&\\
\underline{+\,\,b}&\\
x&
\end{align}
$$
The Associative law of addition
It says that when we add three numbers, it does not matter which two numbers we add first:
P1. \(a + (b + c) = (a + b) + c\)
Since regrouping does not affect the result of addition, we usually omit the parentheses but, in reality, the parentheses are implicitly there; it just happens that it does not matter where they are. For example, it does not matter if we mean
$$a + b + c = (a + b) + c$$
or
$$a + b + c = a + (b + c)$$
because in both cases the result is the same. From here we get that
$$
\begin{align}
a + b + c + d & = ((a + b) + c) + d \\
& = (a + (b + c)) + d \\
& = (a + b) + (c + d) \\
& = a + ((b + c) + d) \\
& = a + (b + (c + d)) \\
\end{align}
$$
Adding two 2-digit numbers
When adding numbers with multiple digits, it is often useful to use a decimal decomposition, e.g.,
$$1234 = 1000 + 200 + 30 + 4$$
We can use this decomposition to simplify additions, e.g.,
$$
\begin{align}
17 + 34 &= (10 + 7) + (30 + 4) \\
&= (10 + 30) + (7 + 4) \\
&= 40 + 11 \\
&= 51 \\
\end{align}
$$
Adding two multi-digit numbers
The U.S. standard addition algorithm adds the digits from right to left, “carrying” sums greater than a digit to the next place value:
$$
\begin{align}
&1\,\,\,\,\,\,\,\,\,1\\
&785,927\\
+\,\,&\underline{262,055}\\
1,&047,982\\
\end{align}
$$
The ‘carry’ is more significant than the number that we are writing under the line; to avoid forgetting to write the ‘carry’, get in the habit of saying, say, 7 + 5 = 12; then write the 12, in that order: first the 1, as a carry, and then the 2, under the line.
Another way to add the numbers is adding by place values; this is longer but avoids errors of forgotten carries.
$$
\begin{align}
&\,\,\,\,\,\,\,785,927\\
&\underline{+\,\,262,055}\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12\hspace{.2in}⇐ 7 + 5\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,70\hspace{.2in}⇐ 20 + 50\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,900\hspace{.2in}⇐ 900 + 0\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,7,\hspace{.48in}⇐ (5 + 2) \times 1,000\\
&\,\,\,\,\,\,\,140,\hspace{.48in}⇐ (80 + 60) \times 1,000\\
&\underline{+\,\,900,\hspace{.45in}}⇐ (700 + 200) \times 1,000\\
&\,1,047,982\\
\end{align}
$$
Writing sums of sequences
When writing a sum of a sequence we usually use dots, or the symbol for a summation:
$$
\begin{align}
\sum_{i = 1}^{10}i &= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10\\
&= 1 + 2 + \dots + 10
\end{align}
$$
The same applies for infinite sums:
$$
\sum_{i = 1}^{\infty}i = 1 + 2 + 3 + \dots
$$
Gaussian addition
An easy way to add sequences of numbers is using Gaussian addition. Say that we want to add the numbers from 1 to 5:
$$1 + 2 + 3 + 4 + 5 = V$$
We can obtain the same result if the write the sequence backwards:
$$5 + 4 + 3 + 2 + 1 = V$$
Now, we pair up the terms of each sum and add the equations to obtain an equation equal to two times our original desired result V:
$$
\begin{align}
(1 + 2 + 3 + 4 + 5 = V)&\\
\underline{+ (5 + 4 + 3 + 2 + 1 = V)}&\\
6 + 6 + 6 + 6 + 6 = 2V&
\end{align}
$$
Because of the symmetry of the columns, the vertical pairs add up to the same number; we simplify the equation to
$$6 \times 5 = 2V$$
and, finally, solve for V:
$$V = \frac{6 \times 5}{2} = 15$$
In general, the sum of all the numbers from 1 to n is
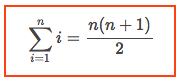
We can use Gaussian addition to add many other sequences. For example, let’s add the odd numbers from 20 to 50:
$$
\begin{align}
(21 + 23 + \cdots + 47 + 49 = V)&\\
\underline{+ (49 + 47 + \cdots + 23 + 21 = V)}&\\
70 + 70 + \cdots + 70 + 70 = 2V&
\end{align}
$$
Since there are 15 odd numbers from 20 to 50, we have that
$$
\frac{70 \times 15}{2} = 525
$$
Yeah? show me.
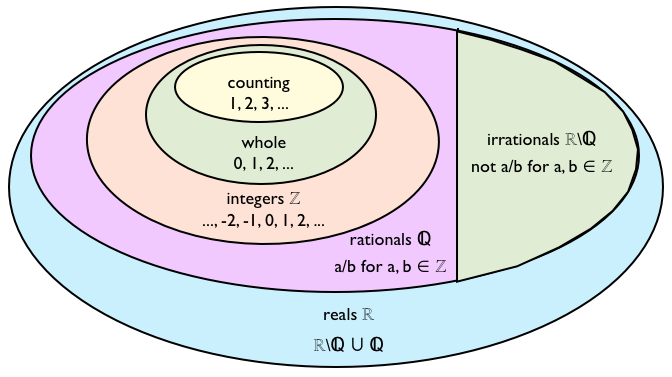
Sets
A set is a collection of things; we can make sets of anything: the set of characters on a page, or the set of children in a room, or the set of animals that fly; each thing in a set is called a member or an element of the set. Sets are useful to group things that share some characteristics, so we can study and understand them better; for example, we can place certain animals into the set of birds, or the set of mammals, or the set of fish. We do the same thing with numbers: to study and understand them better, we divide them in sets, like
Natural numbers (a.k.a. ℕ): we use them to count, like 1, 2, 3,…, etc. There is no universal agreement about whether the natural numbers should include 0 so we have the following more specific sets:
- Whole numbers (a.k.a. non-negative integers) = {0, 1, 2, 3, …}
- Counting numbers (a.k.a. positive integers) = {1, 2, 3 …}
Integer numbers (a.k.a. ℤ, from the german word “Zahlen” that means “to count”): This set contains numbers with no fractions, i.e., the zero, the counting numbers and their negatives:
$$
ℤ = {… -3, -2, -1, 0, 1, 2, 3, …}
$$
Rational numbers (a.k.a. ℚ, from the word “Quotient”): These numbers are ‘rational’ because they come from ‘ratios’. This set contains all the numbers that are ratios of two integer numbers, and all their corresponding decimals, whether their representation is finite, or periodic infinite. Some examples are:
- 0 = 0/1
- 5 = 5/1
- -1/2 = -0.5 (finite decimal)
- 1/3 = 0.33333.. (infinite periodic decimal)
- 1/7 = 0.14285714285714285… (infinite periodic decimal)
Irrational numbers (a.k.a. ℝ\ℚ, meaning ‘real minus rationals’): This set contains all the numbers that are not the ratio of two integer numbers; all their decimal representations are infinite and non-periodic. Some examples are:
- \( \sqrt{2} = 1.4142135623730951… \)
- \( \sqrt{3} = 1.7320508075688772… \)
- \( \pi = 3.141592653589793… \)
- \( e= 2.718281828459045… \)
- \( (1 + \sqrt{5})/2 = 1.618033988749895… \) a.k.a. the golden ratio
Real numbers (a.k.a. ℝ): This set contains all the rationals and irrationals, i.e., all the numbers in the number line.
In summary we have the following relationship:
Problems
1. Add
5 + 3
8 + 9
3 + 8
7 + 5
2. Add using decimal decomposition
12 + 34
74 + 15
19 + 83
49 + 72
3. Add using decimal decomposition
79 + 145
127 + 63
734 + 125
251 + 84
4. Add using both the U.S. standard and decimal decomposition algorithms
$$
\begin{align}
&1,234,567\\
+\,&\underline{2,468,013}
\end{align}
$$
5. Find the following sum using both term-by-term addition and Gaussian addition.
$$
1 + 2 + \dots + 10 = ?
$$
6. Use Gaussian addition to add the odd numbers from 10 to 50
$$
11 + 13 + \dots + 49 = ?
$$
7. Find \( f + g \) for
f = 2x + xy + 4
g = 4x – xy + y + 5
“take all the time you want” problems:
For the following problems use…
P1. \( a + (b + c) = (a + b) + c \)Associativity
to show that …
8. \( ((p + q) + r) + s = p + (q + (r + s)) \)
9. \( (p + (q + r)) + s = (p + q) + (r + s) \)
Challenge – mental math
Simplify before adding
We want to find $a+b = c$. The result $c$ doesn’t change if we add $0$ to $a+b$, and $0$ is simply the addition of a number and its opposite, i.e., $d + (-d) = 0$. Hence:
$$
\begin{align}
c &= a + b\\
&= (a + b) + 0\\
&= (a + b) + (d + (-d))\\
&= (a + d) + (b + (-d))\\
\end{align}
$$
We can simplify additions by choosing $d$ wisely, in a way that simplifies one of the operands. For example, to add $494 + 337$, we can add $d=6$ to $494$ and $d=(-6)$ to $337$; this turns 494 into 500, and simplifies the sum:
$$
\begin{align}
494 + 337&= (494 + 6) + (337+(-6))\\
&= (494 + 6) + (337-6)\\
&= 500 + 331\\
&= 831
\end{align}
$$
Likewise,
$$
\begin{align}
503 + 215&= (503 +(-3)) + (215+3)\\
&= (503 – 3) + (215+3)\\
&= 500 + 218\\
&= 718
\end{align}
$$
We are moving a portion of one of the operands to the other.
Adding left to right
We add the numbers in each column; if the sum of the digits in the column to the right is greater than ten, then add one more. For example:
$$
\begin{align}
&\,\,\,\,\,\,\,785,007\\
&\underline{+\,\,262,015}\\
&\,\,\,10\,\,\,\,\,\,\,\,\,\hspace{.48in}⇐ (7+2) + 1 \mbox{ (add 1 because }8+6\ge 10\mbox{)}\\
&\,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\hspace{.2in}⇐ 8 + 6 = 14 \mbox{ (discard the 1)}\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,7\,\,\,\,\,\,\,\,\,\,\,\hspace{.2in}⇐ 5 + 2 = 7 \mbox{ (don’t add 1 because }0 + 0\lt 10\mbox{)}\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\hspace{.2in}⇐ 0 + 0 = 0 \mbox{ (don’t add 1 because }0 + 1\lt 10\mbox{)}\\
&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\hspace{.2in}⇐ (0 + 1)+1 = 2 \mbox{ (add 1 because }7+5\ge 10\mbox{)}\\
&\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2}\hspace{.15in}⇐ 7 + 5 = 12 \mbox{ (discard the 1)}\\
&\,1,047,022\\
\end{align}
$$
The result of the sum of each column has to fit in the number of places of the result. All the results are constrained to one digit, except for the left-most result which can use two. That is why we discard the 1’s of every column sum except for the left-most column, if any.
Try to add from left to right the numbers that we added in the previous section:
$$
\begin{align}
&\,\,\,\,\,\,\,494\\
&\underline{+\,\,337}
\end{align}
$$
and
$$
\begin{align}
&\,\,\,\,\,\,\,503\\
&\underline{+\,\,215}
\end{align}
$$
If it went well, try to add
$$
\begin{align}
&\,\,\,\,\,\,\,934,532,520\\
&\underline{+\,\,740,629,157}
\end{align}
$$